Cet cours de mesures et incertitudes est distiné pour les élèves de la classe de première C et D. Notez qu’il s’agit d’une note de cours récapitulative qui devrait vous donner une idée de base de ce sujet en physique.
Introduction
Mesurer une grandeur n’est pas simplement rechercher la valeur de cette grandeur mais aussi lui associer une incertitude afin de pouvoir qualifier la qualité de la mesure. Cette incertitude est associée aux erreurs de mesures qui peuvent être dues à l’instrument de mesure, à l’opérateur ou à la variabilité de la grandeur mesurée.
L’incertitude de mesure est la valeur qui caractérise la dispersion des valeurs qui peuvent être attribuées à la grandeur mesurée. On la note u.
I. L’erreur de mesure aléatoire
Lorsqu’un même opérateur répète plusieurs fois, dans les mêmes conditions, le mesurage d’une même grandeur, les valeurs mesurées peuvent être différentes. On parle alors d’erreur de mesure aléatoire.
L’incertitude associée est une incertitude de répétabilité dite de type A.
Une incertitude de type A est évaluée par des méthodes statistiques qui mettent en jeu la moyenne et l’écart-type. Elle est issue de l’exploitation d’un nombre important de valeurs mesurées.
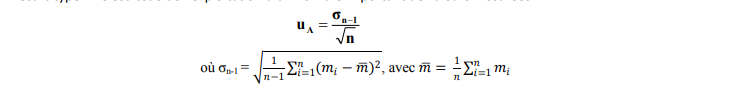
Dans la pratique, on ne peut réaliser qu’un nombre limité de mesurages. Pour prendre en compte ce nombre limité, on multiplie l’incertitude-type par un facteur k appelé facteur d’élargissement.
![]()
Pour un intervalle de confiance de 95%, k vaut environ 2 lorsque n est de l’ordre de 20.
II. L’erreur systématique
Lors d’une mesure unique, la précision de l’appareil de mesure, la façon dont il est utilisé et la qualité du mesurage sont à prendre en compte : l’erreur correspondante est l’erreur systématique et l’incertitude associé est dite de type B.
L’évaluation de celle-ci nécessite de rechercher toutes les sources d’erreur et d’évaluer l’incertitude associée à chaque source.
Pour les incertitudes de type B, on considère que l’incertitude de mesure à prendre en compte est l’incertitude élargie UB = 2uB, pour un niveau de confiance de 95%.
– Lecture sur une échelle graduée :
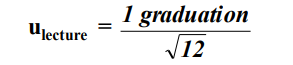
– Double lecture :
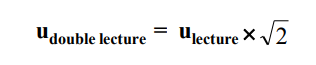
– Utilisation d’un appareil de tolérance donnée (voir notices des appareils) :
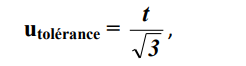
où t est la tolérance de l’appareil (x% de la valeur lue)
– Appareil numérique (voir notices des appareils) :
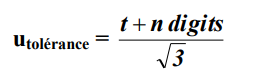
III. Incertitude type composée
Lors d’un mesurage, la détermination de l’erreur de mesure nécessite de prendre en compte les deux composantes précédentes.
Dans le cas où l’on dispose d’une série de mesures et que chacune d’entre elles est affectée d’une incertitude de type B, on obtient l’incertitude-type composée :
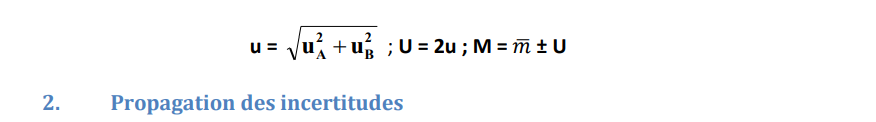
Lorsque X se déduit par calcul à partir de Y et Z connues avec une incertitude-type, la valeur de X est elle aussi entachée d’incertitude. Le calcul de u(X) se fait à partir de u(Y) et u(Z).
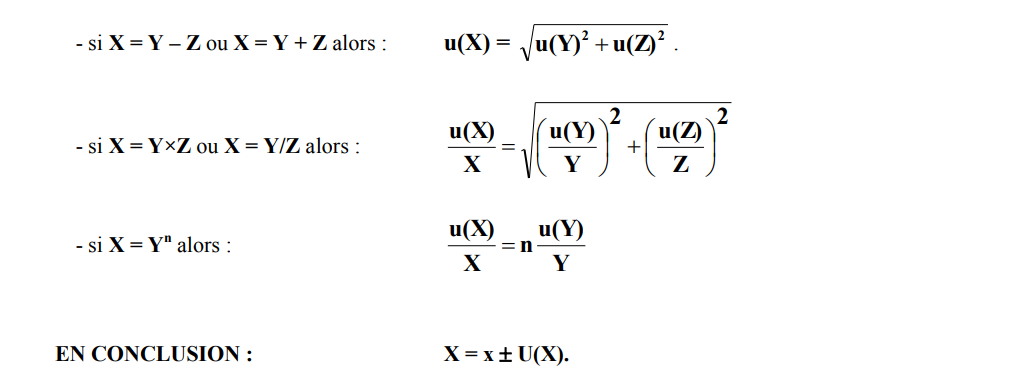
– x est le résultat de(s) la mesure(s) (lecture sur l’appareil ou moyenne des mesures),
– U(X) est l’incertitude élargie à 95% de confiance.
Par convention, l’incertitude est arrondie à la valeur supérieure avec au plus deux chiffres significatifs, et les derniers chiffres significatifs conservés pour la valeur mesurée m sont ceux sur lesquels porte l’incertitude U.



