This short lesson note covers the theory of radioactive decay and the radioactive decay formula. We will also touch points like the activity and he half-life of radioactive decay.
Radioactive decay is purely a random process. It is not possible to predict which nucleus is going to disintegrate next.
Also, it should be noted that radioactive decay cannot be speed-up or slow down. It follows that for large numbers of any particular species, of nuclei, the rate of decay is proportional to the numbers of parent nuclei present.
We saw in the last lesson notes that Radioactivity is the spontaneous (random) emission of radiation from the nuclei of unstable atoms to form more stable nuclei.
The radioactive decay theory
During a radioactive decay process, if there are N parent nuclei at a time t, the rate of decay of N atoms is given by:
As more disintegrates, the number left reduces, so, dN/dt is a reducing quantity.
Therefore, we can say;
, Which implies the rate of decay depends on the numbers of atoms, N left.
From the above proportianality, we can therefore write;
where
is a positive constant of proportionality called the decay constant.
Activity of a radioactive process
The Activity, in radioactive-decay processes, the number of disintegrations per second, or the number of unstable atomic nuclei that decay per second in a given sample. The unit of measurement of the Activity of any radioactive decay process is the Becquerel(Bq) and 1Bq equals a disintegration per second.
The activity is thus given by the formula:
, Where A is the activity, N the numbers of particles and t the time.
The radioactive decay equation
During a radioactive decay, at the time t = 0, the numbers of particles N is N0
To remove the integration, we proceed as follows;
The above equation expresses the nature of radioactive decay. It gives the number of nuclei remaining after a time t and that this number decreases exponentially with time as shown below.
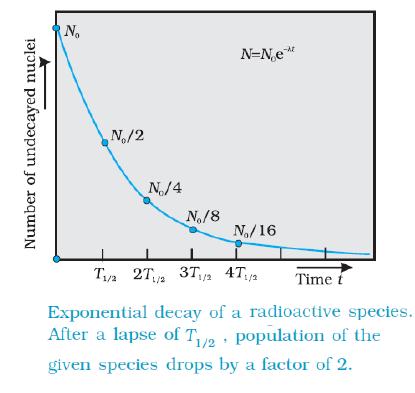
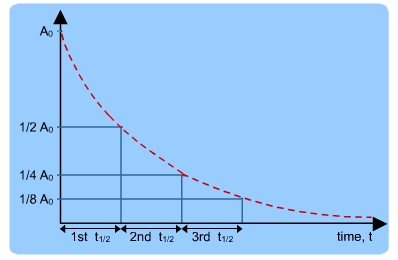
The Half life
Half life is the time taken by a radioactive nucleus to disintegrate to half its original value.
For example, let’s consider the exponential law of radioactive decay
The time taken t for the numbers of nuclei N to reduce to half its original value N0 is given by;
If t at half the original number of nuclei be T1/2, then at
The above equation is called the half life of radioactive nuclei where is measured in seconds.
The relationship between shows that
and
are inversely proportional. A material of long half life decays slowly than the one with a short half life.
The half life of a sample is constant and can be obtained from its exponential curve.